Decision Tree Analysis
for the Risk Averse Organization1
Introduction
The decision tree analysis technique for making decisions in the presence of uncertainty can be applied to many different project management situations. For instance: Should we use the low-price bidder? Should we adopt a state-of-the-art technology? While making many decisions is difficult, the particular difficulty of making these decisions is that the results of choosing from among the alternatives available may be variable, ambiguous, unknown or unknowable.
This paper summarizes the traditional decision tree analysis based on expected monetary value (EMV) and contrasts that approach to the risk averse organization’s use of expected utility (E(U)). Simple examples are provided to illustrate the different approaches. Finally, some suggestions are made to help the decision analyst discover the organization’s utility function. (This paper expands upon Hulett and Hillson, forthcoming)
Standard Decision Tree Criteria –
Expected Monetary Value
Because the consequences of each decision are not known with certainty, the choice of the most beneficial decision and its value is typically calculated based on the values of each possible result multiplied by the probability of that result. Thus, the standard presentation of decision tree analysis bases the decision on the expected monetary value (EMV) of the alternatives. (see PMI, 2004) The rational organization, it is suggested, will decide on the option that offers the highest EMV.
EMV may be best decision criterion for an organization with a lot of projects or for a large organization that is financially stable enough to take the long view. That view might be characterized as: “If it does not work this time, it’ll work on average over our portfolio of projects or over a decade of projects.” In other words, the EMV criterion is not for every organization.
Risk Aversion Decision Making –
Why Use Expected Utility?
Most organizations realize that they do not do the same project many times over and over again. They perform the project only once and therefore have only one chance to “get it right.” Knowing this, they immediately see problems with relying on the average or expected result represented by the EMV to make the correct decision and to value the project:
- There is no assurance that their specific project will have the average result.
- They may be more concerned with the possibility of failure or significant loss than they are enamored with the possibility of the up-side potential.
It is at this point that we need to realize that decision tree analysis methodology and the tools that implement it do not require the use of EMV. Decision trees can be solved based on an expected utility (E(U)) of the project to the performing organization. There is no requirement that utility is measured by EMV. In fact, non-linear utility functions can be substituted for linear EMV in most decision tree software packages, and E(U) is then substituted for EMV as the decision criterion.
There is a trick to analyzing the E(U) of the choices, of course. How do we know the organization’s utility function? We know how to calculate the EMV of alternative bets and their values: multiply the alternative values by their probabilities. However, if utility is not equal to the economic value of the outcome, how do we identify the utility of each scenario to the organization in order to take its expected value? We substitute utility for value and decide on E(U) rather than on EMV.
Simple Decision –
One Decision Node and Two Chance Nodes
We can illustrate standard decision tree analysis by considering a common decision faced on a project. We are the prime contractor and there is a penalty in our contract with the main client for every day we deliver late. We need to decide which sub-contractor to use for a critical activity. Our aim is to minimize our expected cost. It is often difficult to argue for using the higher-priced sub-contractor, even if that one is known to be reliable. The lower-bidding sub-contractor also promises a successful delivery, although we suspect that he cannot do so reliably. A rigorous analysis of this decision using a simplified decision tree structure that minimizes our expected cost is shown below:
- One sub-contractor is lower-cost ($110,000 bid). We estimate however that there is a 50% chance that this contractor will be 90 days late and our contract with the main client specifies that we must pay a delay penalty of $1,000 per calendar day for every day we deliver late.
- The higher-cost sub-contractor bids $140,000. We know this contractor and assess that it poses a low 10% chance of being late, and only 30 days late at that. Of course, our customer will impose on us the same $1,000 delay penalty per day for late delivery.
We need to know if there is any benefit to using the higher-cost sub-contractor, and we suspect it may lie in the greater reliability of performance we expect. Of course, both we and our customer need to be convinced of the benefit. A formal analysis using decision trees will ascertain if there is a benefit, and will also document it for the customer.
In Figure 1 below we see that under some circumstances, usually based on the probabilities, costs and rewards of uncertain events, there could be a rationale leading to hiring the high bidder. We build the structure of the decision tree shown below (For the mechanics of solving the decision tree, see: Hulett and Hillson, forthcoming. The decision tree software used in this paper is Precision Tree® from Palisade Corporation.)
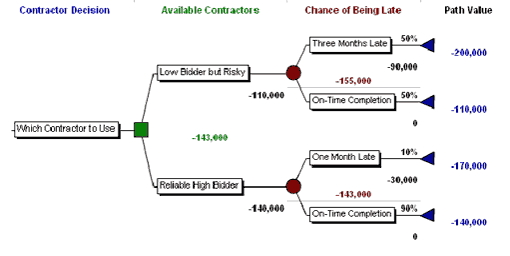
Risk Averse and Risk Neutral Organizations
Expected Utility vs. Expected Monetary Value
In the example above we have assumed that the organization wants to choose whichever decision maximizes its expected monetary value or minimizes its expected cost. This behavior, which could be called “risk-neutral,” may represent an organization that has many projects or takes the long-term view and can thrive if it succeeds “on the average.”
Many, if not most, organizations are cautious in situations where they think they might be vulnerable to large losses. These organizations may shy away from project decisions which, if they were to fail, would expose the organization to large losses, even if such project decisions might also offer a possibility of large gains associated with success. This behavior might be called “risk-averse.” Decisions made by risk-averse organizations’ tend to maximize their E(U) rather than EMV, and that utility may give serious (negative) weight to the possibility of large losses. Most decision tree software allows the user to design a utility function that reflects the organization’s degree of aversion to large losses.
The risk averse organization often perceives a greater aversion to losses from failure of the project than benefit from a similar-size gain from project success. For this organization, the fear of losing $1 million far overweighs the benefit of gaining $1 million. The risk averse organization will not do a project if the chances are 50 – 50 between the two outcomes. The preference for avoiding large losses is quite strong and may outweigh the benefit of gaining the same amount or more. (A similar treatment can be found in Piney, 2005).
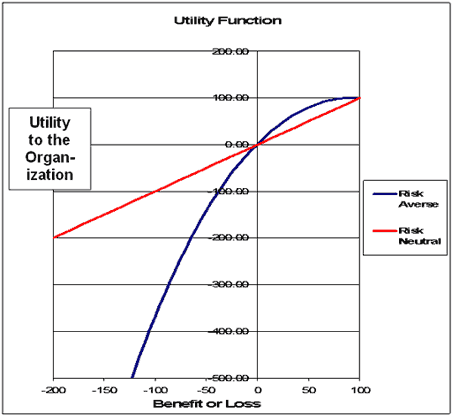
The comparison of the way risk-neutral (EMV) decision-making and risk averse (E(U)) decision-making organizations is shown in figure 2. It shows two organizations’ evaluation of the benefit or loss from different results.
- The straight line (linear utility) represents the way a risk-neutral organization would value the benefit or loss. Notice that the utility (vertical or Y-axis) value associated with the benefit of $100 (on the horizontal or X-axis) is $100. Conversely, the value to this organization that is associated with a loss of $100 on the X-axis is minus $100 on the Y-axis. For this organization, the value of benefit and loss is simply the dollar amount of that benefit or loss.
- The curved (non-linear) utility function shows the utility of an example risk averse organization.1 That organization, as an illustration of just one of an infinite number of possible utility curves, values a gain of $100 at +100 “utils”, but a loss of $100 as minus 369 utils. For this organization, the value of a benefit or loss is not the monetary value, but it is filtered through a non-linear utility function.
Valuing the Project with Uncertain Outcomes
Risk Averse and Risk Neutral Organizations
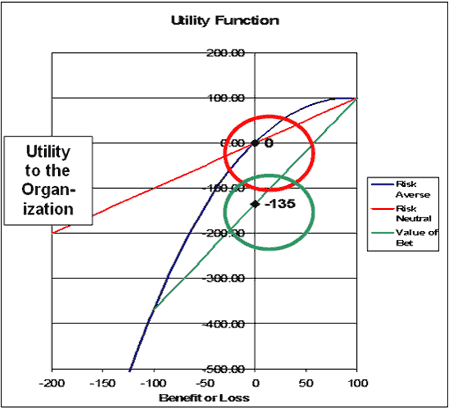
Figure 2 can be used to calculate the value of a wager or chance node in a decision tree when the possible outcomes and their probabilities are known. The difference between a risk neutral and risk averse organization facing the same outcomes and probabilities is shown in Table 1 below:
| Compare Risk Neutral and Risk Averse Organizations Response to an Opportunity to Win or Lose $100 with Equal Probability | |||
|---|---|---|---|
| Alternative Outcome | Value for the Organization | ||
| Value | Probability | EMV | E(Utility) |
| $100 | 50% | 100 | 100 |
| -$100 | 50% | -100 | -369 |
| EMV or E(U) | 0 | -135 | |
Notice that the risk neutral organization, one that values its uncertainty on the EMV model, is indifferent to making or not making a wager that has symmetrical +$100 and -$100 possible outcome. The risk averse organization would be strongly adverse to taking that decision because the negative utility of the possible loss of $100 is -369 utils and the positive utility of the possible gain is only + 100 utils. The 50-50 weighting of those two outcomes results in a negative value for the entire opportunity. This result can be seen on Figure 3 below, where the result is found on the line between the value of utility at +$100 and -$100 on the X axis that matches the relative probabilities:
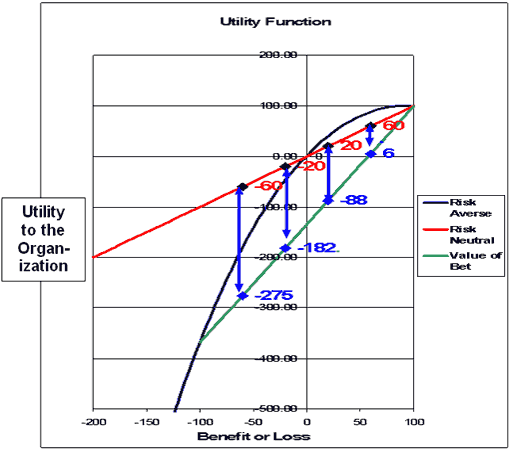
Other combinations of values and probabilities can be evaluated using the chart. Table 2 shows alternative wagers or bets (ventures with uncertain outcomes) that have the same value of outcome but differ as to the probability of each. These would show as different points on the utility curves.
| Compare Risk Neutral and Risk Averse | |||
|---|---|---|---|
| Pr(100) | Pr(-100) | Utility | EMV |
| 80% | 20% | 6 | 60 |
| 60% | 40% | -88 | 20 |
| 40% | 60% | -182 | -20 |
| 20% | 80% | -275 | -60 |
Note from the results of Table 2, the Risk Averse organization would barely accept the wager if it had an 80% chance of success, and it would reject the wager if it has “only” a 60% chance of success. These results are found on Figure 4 by varying the place on the line representing the different wagers by their relative probabilities of the end-points. The vertical lines show how the risk-neutral and risk-averse organizations’ evaluations of the projects or wagers are different. Positive EMV or positive E(U) will lead to those organizations accepting the project while negative values lead to rejection. Over a fair range of relative probabilities the two organizations’ decisions will be different. A decision analyst needs to know which utility function applies to his or her organization in order to make recommendations that are consistent with the organization’s attitudes toward risk.
Discovering the Utility Function of the Organization
The decision or risk analyst should make recommendations about project decisions for an organization based on its own degree (including none) of risk aversion. Any decision facing the organization can be analyzed best if the organization’s attitude toward project risk is known and represented in the analysis by the appropriate utility function. The first job of the risk analyst, then, is to discover the organization’s utility curve independent of any particular project.
It is difficult to discover the organization’s utility function by directly asking people whether they are risk averse and their degree of risk aversion. The best way to uncover the organization’s utility function is to face it, or its leaders, with alternative ventures or projects with some assumed resulting payouts / costs scenarios and probabilities of those alternatives. The leaders can then examine their decision-making process and determine whether they would take on those projects or “pass” on them. It is best if this endeavor is conducted away from the pressures of daily governance, perhaps offsite with as few interruptions as possible. Also, the alternative ventures should be chosen with some care:
- The sample scenarios should be relevant to the organization and decisions to be made. That includes being of the right magnitude (e.g., if it is a large company, make the payoffs and costs in the millions or hundreds of millions of dollars) and in the same general context as the decision to be evaluated.
- The sample scenarios should span the range of the business decisions to be analyzed. This includes examples with probabilities that encompass the probabilities found in the subject decision (e.g., if some scenarios are 60% likely, then some of the examples should include scenarios in that range).
The reason for taking such care in crafting the sample scenarios for the organization’s leaders to ponder is that we are trying to discover the shape of the utility curve around the probability and magnitude of the real decisions to be analyzed. The utility curve we construct is more likely to be accurate if the decision is within range of the sample scenarios and interpolated from the discussion with the organization’s leaders than if it is outside of those scenarios and extrapolated beyond the range examined by them.
After discussing the way the organization would choose when faced with various uncertainties, costs and rewards, the analyst has the raw material needed to craft the organization’s utility function. By determining how the organization would act in a few, e.g., 6 to 10 different scenarios the analyst can then try to find a utility function in the decision tree software that matches the various decisions. Alternative specifications are available in each software package. The analyst will experiment with the various types of utility functions (e.g., logarithmic, exponential) and scaling offered by the software until many of the results are consistent with those that the organization’s leaders said they would make in similar circumstances.
A simple example of this examination might include the following example (Figure 5): An organization will be asked to embark on a project with a risk of gain and loss and its probabilities. Will it accept that project or not? In the figures that follow, it is initially not clear whether the organization is following a linear or risk-neutral utility function or a non-linear risk-averse one.
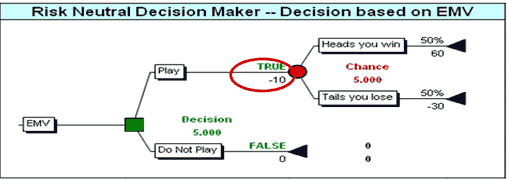
Put this scenario to another organization and it may undertake the project even if it is risk averse. Figure 6 below shows that a decision to take on this project may be logical even for a risk averse organization.
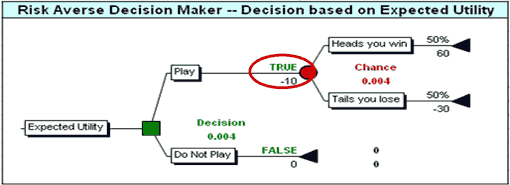
The question then becomes: How do we determine for these two organizations (in Figures 5 and 6) whether they are using a linear risk neutral or a non-linear risk averse utility function? One way to do this would be to change the scenario and see whether the organization would reject the project with an increase in the possible loss, even though the new scenario still results in a positive EMV. That result, rejecting a project with a positive EMV, would be an indication of a risk-averse organization.
In Figure 7, below, the costs and rewards are multiplied by a factor of 10, but the probabilities are the same. The same utility function used in Figure 6 is applied and the result is different. Although the EMV is still positive (EMV = $50 million), the risk-averse utility function results in rejecting this project. Apparently, the 50% prospect of losing $300 million is more daunting for the organization than the 50% prospect of losing $30 million, and the larger EMV ($50 million for Figure 8 vs. $5 million for Figure 7) is not sufficient to make this project attractive to the organization’s leaders.
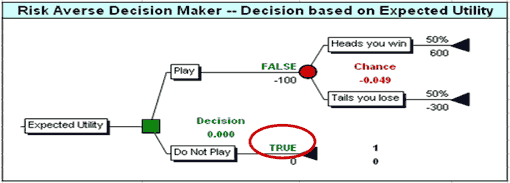
Designing various appropriate scenarios and getting the organization’s leaders in a room to discuss them is difficult enough. In practice the leaders will not have a unified or consistent view of their own utility function. Often these leaders will make decisions that cannot be fit into any available utility function. This result may occur when the leaders actually have different utility functions among them, and the decisions are based on some type of voting (formal or informal). When this happens, the analyst should return to the leaders and point out the inconsistency of their decisions and determine if they want to revisit the decisions that do not fit within the most reliable utility function available. This exercise has the potential of making the organization’s decisions more logical and thoughtful (it may also shorten the professional life of the analyst).
Ultimately, the utility function that fits most of the decisions on the example scenarios can be used in future decision analyses for the organization.
Conclusion
Project decisions, even quite simple ones, can be difficult to make because their implications are often not certain. This is a fact of life for most project managers, who often face situations like those explored above: the choice of alternative contractors and of alternative technologies. Each of these decisions poses clear alternatives but murky consequences.
Uncertain consequences are best described and analyzed using probability concepts as part of a decision tree analysis.
Two alternative approaches are shown in this paper. We use “risk neutral” to describe those organizations that make decisions based on maximizing Expected Monetary Value or minimize expected costs to the organization. We use “risk averse” to describe those that use a non-linear utility function and maximize E(U). It is clear that some decisions with positive EMV may have negative E(U). In those circumstances, rational organizations may differ on their decisions.
A challenge to the decision analyst is to discover the utility function (liner or non-linear) of the organization. We have proposed a set of experiments for the organization’s leaders to give the decision analyst material from which the utility function can be derived. This experiment, or workshop, may yield some interesting results about the internal consistency of the organization’s decision-making process.
References
Hulett, David and David Hillson, Use Decision Trees to Make Important Project Decisions, PM Network, May 2006 (© PMI)
Project Management Institute. (2004) A guide to the project management body of knowledge (PMBOK®) (3rd ed.). Newtown Square, PA: Project Management Institute, Chapter 11 Risk Management
Piney, Crispin, (2003), Applying Utility Theory to Project Risk Management, Project Management Journal, 2003
- 1There are many different utility functions and this is just an example of one. They usually show diminishing returns to benefits and increasingly-large negative returns to penalties. Hence, they are nonn-linear.
Link to the pdf file: Decision Tree Analysis for the Risk Averse Organization.pdf


